Real polymers
How can we model real polymers with KG polymer models?
A polymer melt has properties such as time dependent shear viscosity/compliance, which is due to the spectrum of relaxation times dictated by the molecular structure. A polymer network has a specific distribution of chain lengths and trapped entanglements, which gives rise to a specific deformation response. The specific experimental results varies with polymer chemistry, molecular structure and state point. Hence inventing a model to capture all these phenomena sounds at first sight very complicated. Recently we published the solution to this problem: ”Kremer Grest Models for Commodity Polymer Melts: Linking Theory, Experiment, and Simulation at the Kuhn Scale.” R. Everaers, H. A. Karimi-Varzaneh, F. Fleck, N. Hojdis, C. Svaneborg. Macromolecules 53, 1901 (2020)
In case you are looking for the online calculator go here "Kuhn Mapping for Kremer-Grest polymer models".
Universality: Fortunately, for the physics that is dominated by the conformational entropy of the molecules universality applies, this includes the physics of viscoelastic material response of polymer melts and polymer networks such as rubber. On the other hand, the physics of the glass transition depends on the specific monomeric interactions and packing, and hence can not be expected to be universal at least not in a Kuhn description. Kuhn's seminal insight was to describe a real polymer as an equivalent random walk with a number of segments, and a step length of each segment such that it matches the mean-square end-to-end distance and contour length of the real polymer.
Concretely this means that we can take any experimental number and make it non-dimensional using the Kuhn length, Kuhn time, and kBT as units for length, time, and energy. Then (for linear polymers) the result can only be a function of two dimensionless numbers NK and nK, where the former is the is number of Kuhn segments per chain which varies from system to system, and the latter is the Kuhn number nk = ρK lK3 which is a dimensionless measure of density.
For example, the entanglement modulus is an emergent property of long entangled melts. Moduli are energy densities, hence the non-dimensional form is Ge lK3 / kBT. This is a special case since theory shows that Ge lK3 / kBT = nK3 / α2 and shows that it depends only on the Kuhn number. α is the number of chains per entanglement volume and is independent of polymer species. Other properties depend both on chain length as well as Kuhn number. Below is shown a figure of reduced entanglement moduli vs. Kuhn number for various polymer chemistries (symbols) and a slightly more sophisticated theory that accounts for stiffness effects.
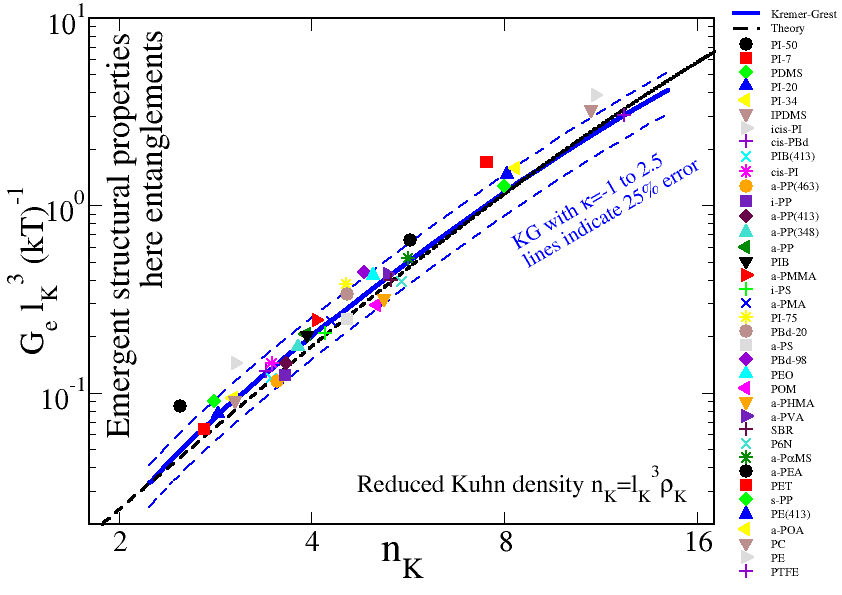
Stiff Kremer-Grest: Since by changing the stiffness of a KG model we can systematically vary the Kuhn number, hence covering the experimental range of polymer stiffneses. By generating numerous highly entangled, well equilibrated polymer melts we can using Primitive Path Analysis to estimate the corresponding entanglement moduli, having previously characterized how the Kuhn length varies with stiffness. We can also make simulation data for the reduced entanglement modulus. These are illustrated by the solid blue curve in the figure above, and as we expected from universality these are in perfect agreement with the real polymers.
Conclusion: The conclusion is that universality does not only apply for real polymers and experimental data, but also apply to realistic polymer models. Hence to simulate any of the experimental polymer systems above, we simply pick a chain stiffness that produce a Kuhn number (same value on x axis) matching that of the real polymer. If we in addition generate model systems with the same number of Kuhn segments as for an experimental target system, then we expect the simulations to make accurate parameter free predictions of ALL experimental results due to universality.
Theory: Theories make simplifying assumptions and often does not include complications such as bead packing and incompressibility. Kuhn matched KG models makes parameter free predictions which include these complications. Hence any deviation between simulations and theory suggest flaws in the theory, and hence allows us to study how to improve the theory.
Atomistics: Atomistic models describe all atoms in a polymer and have time steps in the fs range. KG model beads roughly corresponds to a monomer and have time steps in the ps-ns range (depending strongly on temperature). Hence the KG models are orders of magnitude faster and enables studies of relatively slow dynamic phenomena (given enough computer power), which are not feasible with atomistic models. On the other hand, atomistic models can be designed to study physics in the glassy regime. While KG models also have a glass transition, the present approach is not expected to be valid close to the glass-transition.
Representability: Due to universality, we expect all entropy dominated physical phenomena to be accurately represented by KG models. Additional effects such as e.g. poly dispersity in chain length or structure, or geometric confinement or filler particles would require additional parameters and energy scales to be introduced in the KG model.
Transferability: Changing temperature is not expected to have a strong effect on the Kuhn number, since both Kuhn length and density are only weakly temperature dependent. If the temperature changes strongly, we can design state-point-specific KG models by matching the Kuhn number at the temperatures of interest, and performing the non-dimentionalization with state specific Kuhn length and time scales. The time mapping is very strongly temperature dependent, and as the real polymer is cooled and dynamics slows down, the KG model simulations are performed at a constant temperature 1 in LJ units, and hence simulation time is stretched exponentially making simulations much faster than real dynamics.
